Distinguish mode dispersion, which is caused by a large number of modes in the optical fiber and the chromatic dispersion associated with the incoherence of light sources actually operating in a certain range of wavelengths.
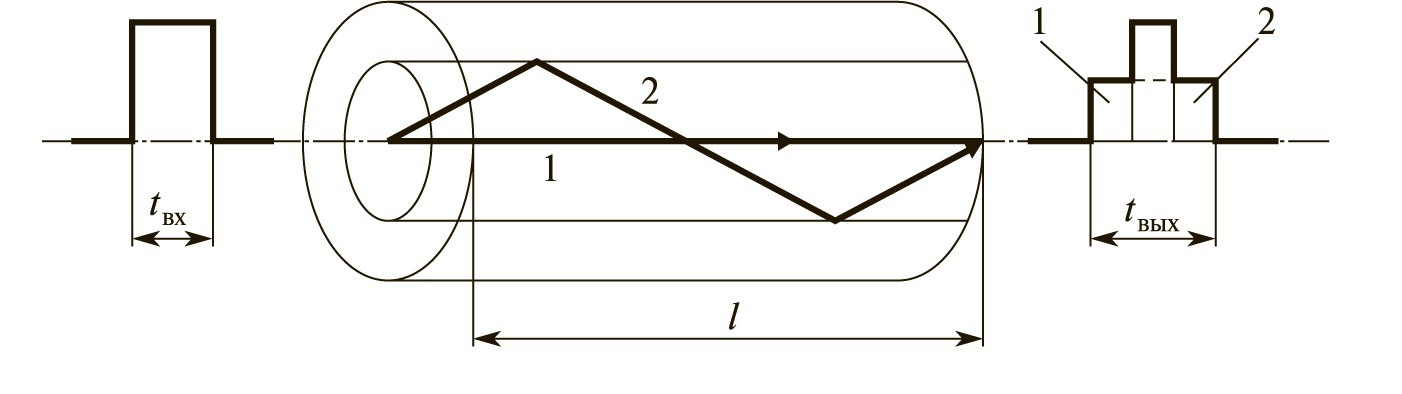
Consider the propagation of the light beam along the multimode fiber. In this case there are two modes, the two beams. The first extends along the longitudinal axis of the fiber, while the other is reflected from the interfaces of media. Thus the path of the second light beam is greater than the first. As a result, when the two beams carrying the electromagnetic energy are added together, compared oblique beam with an axial beam is the time delay, which is calculated by the following formula:
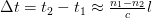
c
– speed of light
l
– fiber length
n
1
,
n
2
– refractive indices of the core and shell
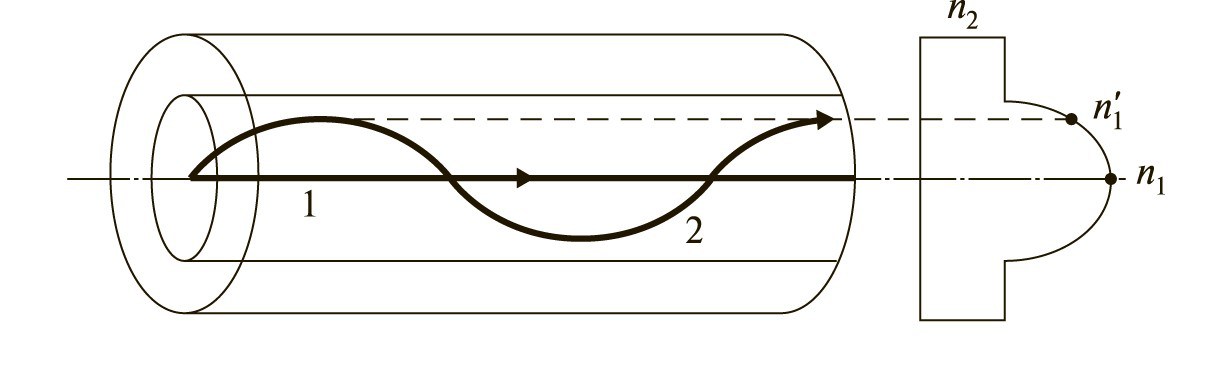
Gradient mode dispersion of optical fibers, usually two orders of magnitude lower than those fibers with a step refractive index profile. Due to the smooth change of the refractive index of the core of an optical fiber decreases the path of the second beam along the fiber. Thereby reducing second time delay relative to the first beam.
The single mode optical fiber mode dispersion, and no increase in pulse duration is determined by the chromatic dispersion, which, in turn, divided into material and waveguide.
Material dispersion phenomenon is called the absolute dependence of the refractive index n material wavelength of light ( n =ϕ λ() ). The waveguide dispersion coefficient is determined by the dependence of the phase β and of the frequency ( β=ϕ ω() ).
Pulse broadening due to chromatic dispersion is calculated using the formula:
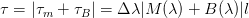
τ
m
– pulse broadening due to material dispersion, ps;
τ
B
– broadening of the pulse due to the waveguide dispersion, ps;
∆λ
– the spectral width of the radiation source, nm;
М(λ)
– coefficient of specific material dispersion, ps / nm · km;
В(λ)
– a coefficient of the waveguide dispersion, ps / nm · km.
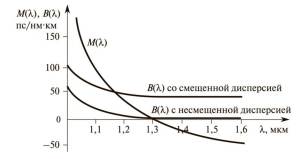
Consider the effect of material and waveguide dispersion in single-mode fiber. As seen from the graph, an increase in the wavelength dispersion of the material decreases, and at a wavelength of 1.31 m it becomes equal to zero. The wavelength in this case is considered a zero-dispersion wavelength. At the same time more than 1.31 micron dispersion becomes negative. Unbiased waveguide dispersion of fibers is a relatively small value and is in the range of positive numbers. In the development of optical fiber dispersion-shifted, which is based on the waveguide component, trying to compensate for the dispersion of the material to longer wavelengths, ie, a third transparent window (λ = 1,55 m). This shift is carried out reduction of the core diameter, increasing Δ and using the triangular shape of the refractive index profile of the core.

In the propagation of polarized light wave along the optical fiber polarization dispersion occurs. The light wave from the standpoint of the wave theory is a constantly changing magnetic and electric field vector which is perpendicular to the propagation of electromagnetic (light) waves. An example of a light wave may be natural light whose direction of electric vector varies randomly. If the radiation is monochromatic and vectors oscillate with a constant frequency, they can be represented as the sum of two mutually perpendicular components of x and y. The ideal optical fiber is an isotropic medium in which the electromagnetic properties are the same in all directions, for example refractive indices. Media with different refractive indices in two orthogonal axes x and y are called birefringent. Thus in this case, the fiber remains single mode for as two orthogonally polarized modes have the same propagation constant. But this is true only for ideal optical fiber.
In a real optical fiber two orthogonally polarized modes have non-identical propagation constants, so that there is a time delay occurs and the broadening of the optical pulse.
The broadening of the pulse due to polarization mode dispersion (PMD) is calculated as follows:
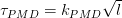
Therefore, the polarization mode dispersion is manifested only in the single-mode optical fibers with netsirkulyarnoy (elliptical) core and, under certain conditions becomes comparable with chromatic. Therefore, the resulting dispersion single mode optical fiber is determined by the following formula:
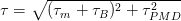
Dispersion significantly limits the bandwidth of optical fibers. The maximum bandwidth on the optical line 1 km calculated by the approximate formula:
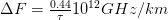
τ — pulse broadening, ps / km.
