Implementation of the Wave algorithm (Lee algorithm) in Java

алгоритм ли, волновая трассировка, волновой алгоритм, Java

Sometimes there is a problem to find the minimum path from point A to point B . The map can have barriers and be like a labyrinth. Similar tasks can be done in game development, PCB design and GPS development, etc.

There is a large set of algorithms for finding the minimum path. The most simple and effective is the Wave trace Algorithm (Lee algorithm). Which is based on the methods of breadth-first search.

This algorithm is not difficult to understand. It will be understandable even for a beginner in programming.

I will give an example of my work. I have a similarity of a cellular automaton (a graph consisting of nodes and edges between them).  It will implement the Lee Algorithm.

The implementation of the algorithm consists of 3 stages:

1. The initialization of the initial data;
2. Wave propagation;
3. Path recovery.

The first step - Initialize the initial data

You need to have an array of objects (nodes, cells). I have this class Node .

Each object has a field of near type, for example, ArrayList.  In this field you write down all the "neighbors" ( neighboring nodes of this node ).

Each node has a check mark available / unavailable.

Start and finish nodes are recorded.

The second stage - Wave propagation

You must have a numeric array (by the number of cells) where the numbers (marks) for each cell will be written. By default, all cell values are zero.

The start node is set to 1.

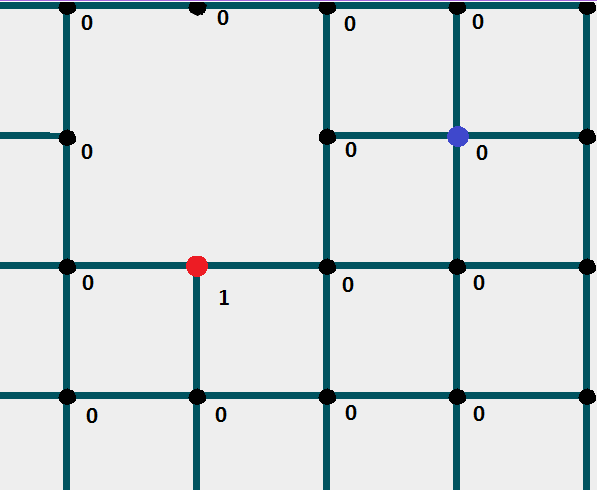
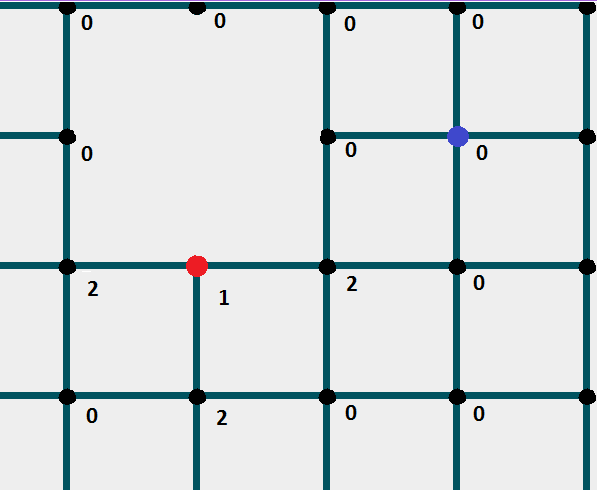
Check all the "neighboring" nodes of this node for "availability", and check whether they already have a mark.

If everything is suitable, put a mark on 1 more than the previous node. Then check its "neighboring nodes".

Continue until you reach the finish cell.

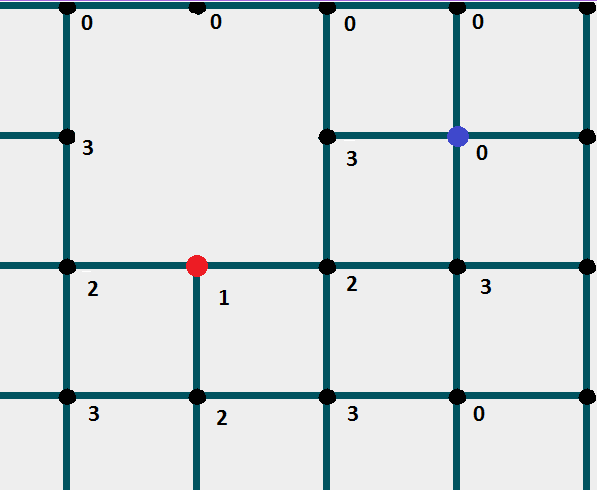
Code example:

public int[] WavePropagation(int fromNode, int toNode, ElementManager elementManager) {  
        int[] markedNode = new int[elementManager.GetNumberOfAllNodes()]; // array where each node's marks will be located
        int markNumber = 1;                        // counter
        markedNode[fromNode] = markNumber;         // initializing the start node
        while (markedNode[toNode] == 0) {          // until you reach the finish node
            for (int i = 0; i < markedNode.length; i++) { 
                if (markedNode[i] == markNumber) {                                          // we start with the starting node
                    for (int j = 0; j < elementManager.GetNode(i).near.size(); j++) {       // looking all the neighboring nodes
                        if(markedNode[elementManager.GetNode(i).near.get(j).number] == 0    // if it has not yet received a mark
                           && elementManager.GetNode(i).near.get(j).isEnable){              // if available
                            markedNode[elementManager.GetNode(i).near.get(j).number] = (markNumber + 1);
                        }
                    }
                }
            }
            markNumber++;
        }
        return markedNode;
    }

The third stage - Path recovery

In the path array, place the finish node.

View the marks of all nodes that are "neighboring" to the final node. Put in the path array that node, the mark of which is 1 less than the finish node.

Repeat this action until the start node is reached.

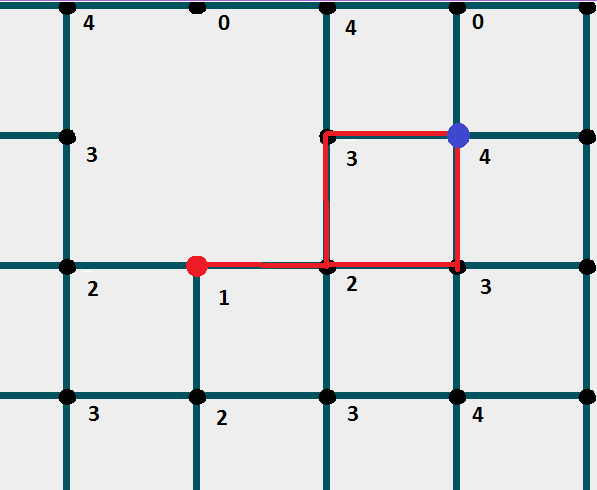
Code example:

public ArrayList<Integer> PathRecovery(int fromNode, int toNode, int[] markedNode, ElementManager elementManager) {  
        ArrayList<Integer> paramsPaveTheRoute = new ArrayList<>();       // array where the path is stored
        if (markedNode[elementManager.GetNode(toNode).number] != 0) {    // once again, check whether the algorithm has reached the finish node
            paramsPaveTheRoute.add(toNode);                              // add the finish node to the path
            ElementManager.Node currentNode = elementManager.GetNode(toNode);
            while (currentNode.number != fromNode) {                     // until we reached the starting node
                for (int i = 0; i < currentNode.near.size(); i++) {      // check the neighboring nodes
                    if (markedNode[elementManager.GetNode(currentNode.near.get(i).number).number]
                            == markedNode[currentNode.number] - 1) {     // if the node's markup value is 1 less than the previous node
                        currentNode = elementManager.GetNode(currentNode.near.get(i).number); //node becomes the current
                        paramsPaveTheRoute.add(currentNode.number);      // entered into array
                    }
                }
            }
        }
        return paramsPaveTheRoute;
    }

The result of the program:

So, I think you've seen that the Wave Trace Algorithm (Lee Algorithm) is not at all difficult to implement. It searches for the minimum path by doing a small number of calculations.  If you want, this universal algorithm can be complicated.