Іноді перед нами постає завдання знайти мінімальний шлях від точки А до точки В . "Карта пересування" може мати перепони та бути подобою лабіринту. Подібні завдання зустрічаються при розробці ігор, проектуванні друкованих плат та розробці GPS-навігаторів тощо.
Алгоритмів пошуку мінімального шляху безліч. Але, найпростішим і найефективнішим є Алгоритм хвильового трасування (Алгоритм Лі) , який заснований на методах пошуку в ширину.
У роботі цього алгоритму не складно розібратися. Він буде зрозумілий навіть новачкові у програмуванні.
Я наводитиму приклад своєї роботи. У мене є подібність клітинного автомата (граф, що складається з вузлів та ребер між ними). На ньому будемо реалізовувати "Алгоритм Лі".
Реалізація алгоритму складається з 3-х етапів:
- Ініціалізація початкових даних;
- Поширення хвилі;
- Відновлення шляху.
Перший етап - Ініціалізація початкових даних
Вам потрібно мати масив об'єктів (вузлів, осередків). У мене це клас Node .
Кожен об'єкт, крім інших, має поле near типу, наприклад ArrayList. У даному полі ви записуєте всіх "сусідів" ( сусідні вузли даного вузла ).
Кожен вузол отримує позначку "прохідний/непрохідний".
Записуються стартовий та фінішний вузли.
Другий етап - Поширення хвилі
Ви повинні мати численний масив (за кількістю осередків), куди записуватимуться числа (позначки) для кожного осередку. За замовчуванням усі значення осередків дорівнюють нулю.
Стартовий вузол
отримує значення 1.
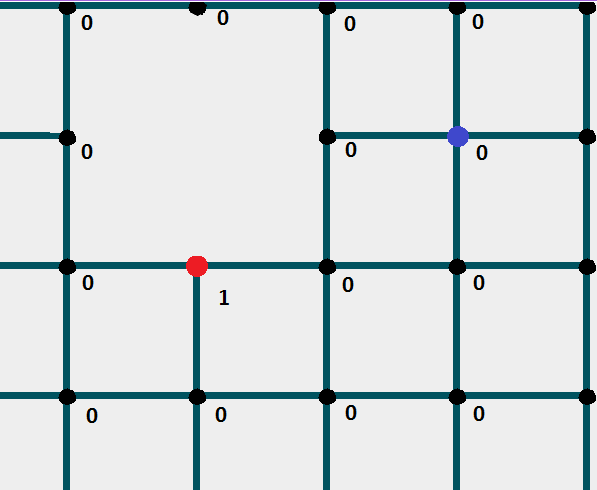
Перевіряєте всі "сусідні" вузли даного вузла на "прохідність", і перевіряєте чи немає на них позначки. Так як позначка має ставитися лише один раз.
Якщо всі задовільно ставите позначку на 1 більше, ніж у попереднього вузла. Далі перевірка його "сусідних вузлів".
Так до тих пір, поки не дійдете до фінішного осередку.
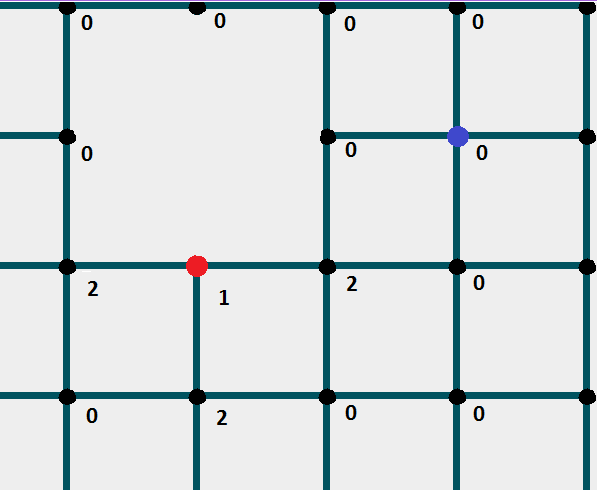
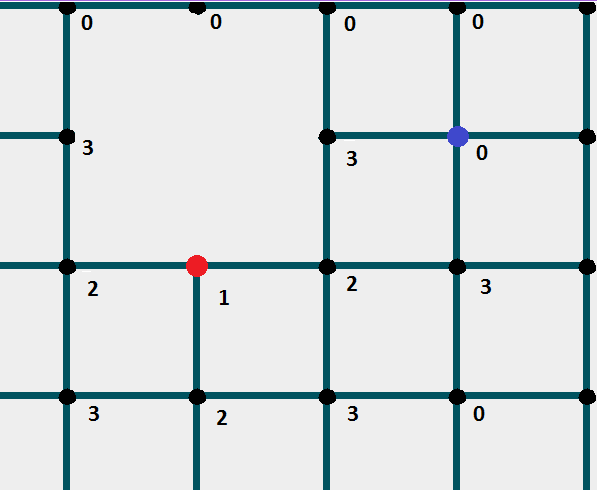
Приклад коду:
- public int[] WavePropagation(int fromNode, int toNode, ElementManager elementManager) { // распространение волны
- int[] markedNode = new int[elementManager.GetNumberOfAllNodes()]; // массив, где будут хранится "отметки" каждого узла
- int markNumber = 1; // счетчик
- markedNode[fromNode] = markNumber; // инициализация стартового узла
- while (markedNode[toNode] == 0) { // пока не достигли финишного узла
- for (int i = 0; i < markedNode.length; i++) {
- if (markedNode[i] == markNumber) { // начинаем со стартового узла
- for (int j = 0; j < elementManager.GetNode(i).near.size(); j++) { // просматриваем все соседние узлы
- if(markedNode[elementManager.GetNode(i).near.get(j).number] == 0 // если он еще не получил "отметку"
- && elementManager.GetNode(i).near.get(j).isEnable){ // если доступен
- markedNode[elementManager.GetNode(i).near.get(j).number] = (markNumber + 1);
- }
- }
- }
- }
- markNumber++;
- }
- return markedNode;
- }
Третій етап - Відновлення шляху
У масив шляху заносите фінішний вузол .
Переглядаєте позначки всіх вузлів, "сусідніх" до фінального вузла. Заносьте в масив шляху той вузол, позначка якого на 1 менше , ніж у фінішного вузла.
Повторюєте цю дію, поки не буде досягнуто стартовий вузол .
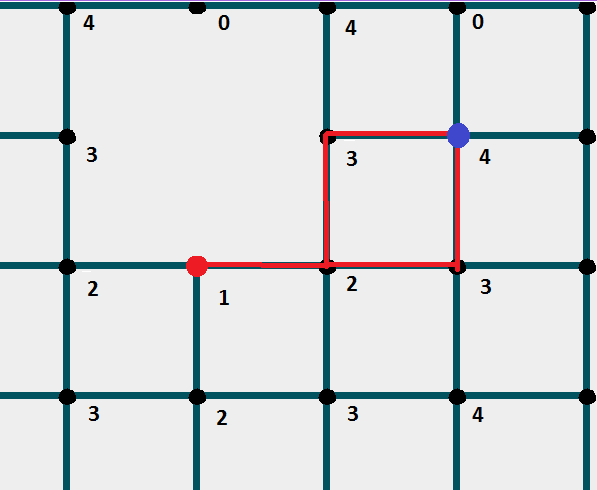
Приклад коду:
- public ArrayList<Integer> PathRecovery(int fromNode, int toNode, int[] markedNode, ElementManager elementManager) { // восстановление пути
- ArrayList<Integer> paramsPaveTheRoute = new ArrayList<>(); // массив, где хранится путь
- if (markedNode[elementManager.GetNode(toNode).number] != 0) { // еще раз проверяем дошел ли алгоритм до финишного узла
- paramsPaveTheRoute.add(toNode); // добавляем финишный узел к пути
- ElementManager.Node currentNode = elementManager.GetNode(toNode);
- while (currentNode.number != fromNode) { // пока не дошли до стартового узла
- for (int i = 0; i < currentNode.near.size(); i++) { // проверяем соседние узлы
- if (markedNode[elementManager.GetNode(currentNode.near.get(i).number).number]
- == markedNode[currentNode.number] - 1) { // если значение пометки узла на 1 меньше, чем у предыдущего узла
- currentNode = elementManager.GetNode(currentNode.near.get(i).number); //узел становится текущим
- paramsPaveTheRoute.add(currentNode.number); // заносится в массив
- }
- }
- }
- }
- return paramsPaveTheRoute;
- }
Результат роботи програми:
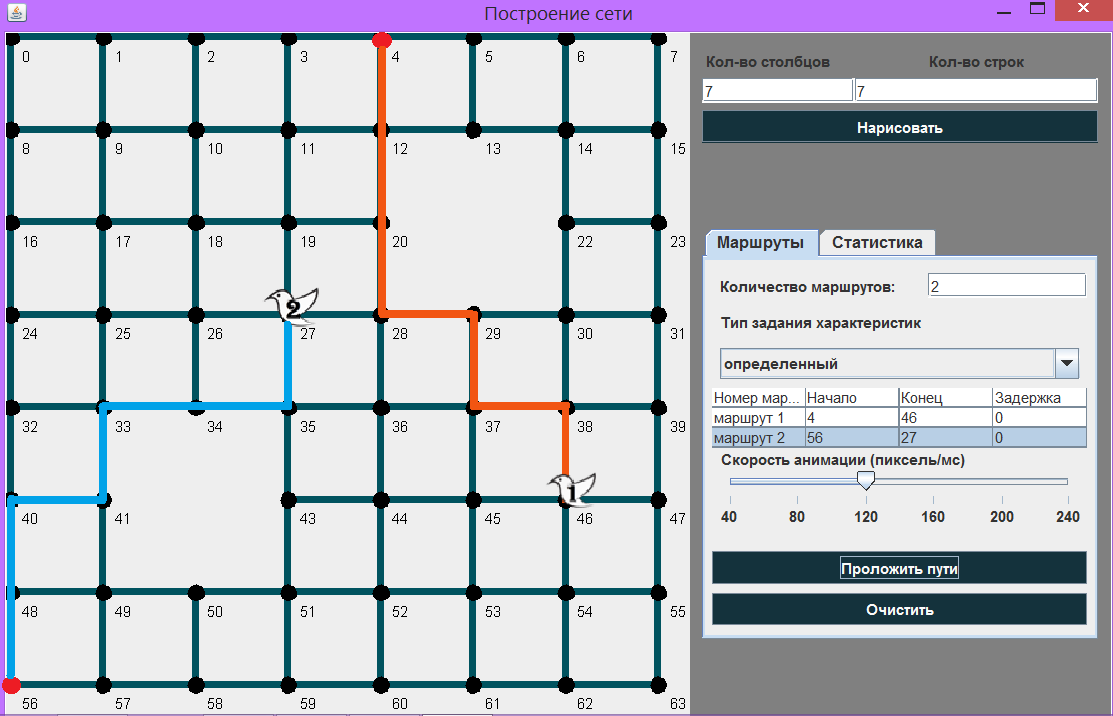
Таким чином, я думаю, ви переконалися, що Алгоритм Хвильового трасування (Алгоритм Лі) зовсім не складний для реалізації. Він виконує пошук мінімального шляху, роблячи невелику кількість обчислень. За бажання, цей універсальний алгоритм можна ускладнити.
