Машинное обучение, Machine Learning, ИИ, AI

Багато статей про алгоритми машинного навчання надають відмінні визначення - але вони не полегшують вибір алгоритму, який вам слід використовувати. Прочитайте цю статтю!

Коли я починав свою подорож наукою про дані, я часто стикався з проблемою вибору найбільш відповідного алгоритму для моєї конкретної задачі. Якщо ви схожі на мене, то коли ви відкриваєте статтю про алгоритми машинного навчання, ви бачите сотні докладних описів. Парадокс полягає в тому, що це не полегшує вибір того, який із них використовувати.

У цій статті для Statsbot я постараюсь пояснити основні поняття та дати деяку інтуїцію використання різних видів алгоритмів машинного навчання для різних завдань. Наприкінці статті ви знайдете структурований огляд основних особливостей описуваних алгоритмів.

Насамперед, слід виділити чотири типи завдань машинного навчання:

1. Навчання з учителем
2. Навчання без вчителя
3. Навчання з частковим залученням вчителя
4. Reinforcement training

Навчання з учителем

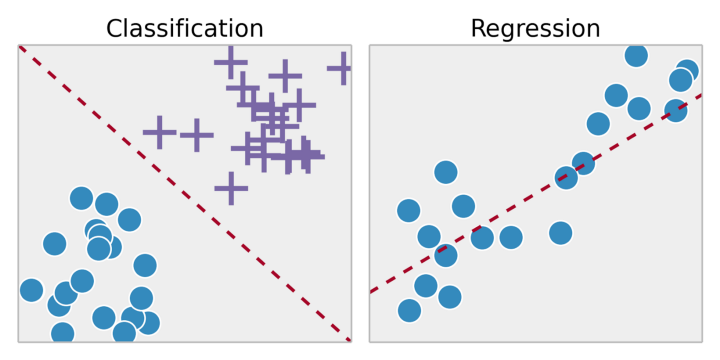
Навчання з учителем є завданням навчання системи на тренувальному наборі даних. Шляхом припасування результатів навчання до тренувального набору даних ми хочемо знайти найбільш оптимальні параметри моделі для прогнозування можливих відповідей на інших об'єктах (тестових наборах даних). Якщо безліч можливих відповідей є дійсним числом, це завдання регресії. Якщо безліч можливих відповідей має обмежену кількість значень, де ці значення є невпорядкованими, це завдання класифікації.

Навчання без вчителя

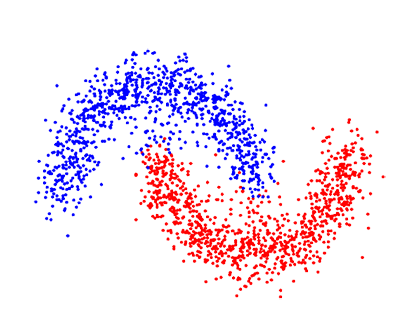
У неконтрольованому навчанні у нас менше інформації про об'єкти. Зокрема, тренувальний набір даних немає маркованих даних, які стосуються певному класу заздалегідь визначених даних. Яка наша ціль зараз? Можливо, спостерігати деяку подібність між групами об'єктів та включати їх у відповідні кластери. Деякі об'єкти можуть сильно відрізнятись від усіх кластерів, і таким чином ми припускаємо, що ці об'єкти є аномаліями.

Навчання з частковим залученням вчителя

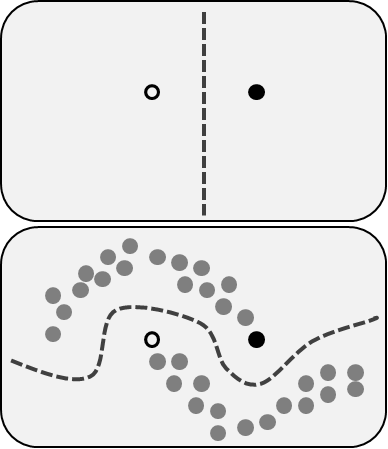
Навчання з частковим залученням вчителя включає обидві проблеми, які ми описали раніше: вони використовують марковані, зумовлені та невизначені, немарковані дані. Це чудова можливість для тих, хто не може редвизначити, маркувати свої дані. Цей метод дозволяє значно підвищити точність, оскільки ми можемо використовувати невизначені дані в тренувальному наборі даних з невеликою кількістю маркованих даних.

Навчання з підкріпленням

Навчання з підкріпленням не схоже ні на будь-яке з наших попередніх завдань, тому що тут ми не маємо ні визначених маркованих даних, ні немаркованих наборів даних. Навчання з підкріпленням - область машинного навчання, пов'язана з тим, як агенти програмного забезпечення повинні робити дії в певному середовищі, щоб максимізувати певне поняття кумулятивної нагороди.

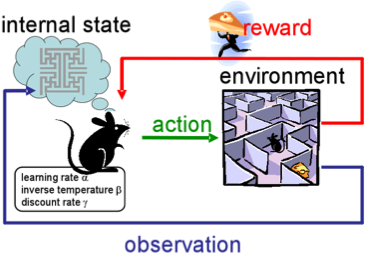
Уявіть, що ви робот у якомусь дивному місці. Ви можете виконувати дії та отримувати нагороди від навколишнього середовища для них. Після кожної дії ваша поведінка стає більш складною і розумною, тому ви тренуєтеся, щоб поводити себе найефективнішим способом на кожному кроці. У біології це називається адаптацією до природного середовища.

Найчастіше використовувані алгоритми машинного навчання

Тепер, коли ми знайомі з типами завдань машинного навчання, розглянемо найпопулярніші алгоритми з їх застосуванням у реальному житті.

Лінійна регресія та лінійний класифікатор

Ймовірно, це найпростіші алгоритми машинного навчання. Ви маєте функції x1, ... xn об'єктів (матриця A) і _мітки (вектор b). Ваша мета - знайти найбільш оптимальні ваги w1, ... wn та зміщення для цих функцій відповідно до деякої функції втрат; наприклад, середньоквадратична помилка або середня абсолютна помилка завдання регресії. У разі середньоквадратичної помилки існує математичне рівняння з методу найменших квадратів:

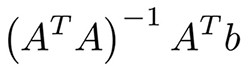
Насправді легше оптимізувати його з допомогою градієнтного спуску, що набагато ефективніше обчислюється. Незважаючи на простоту цього алгоритму, він працює дуже добре, коли у вас тисячі функцій; наприклад, набір слів чи n-грамів під час аналізу тексту. Більш складні алгоритми страждають від перепризначення багатьох функцій, а чи не величезних наборів даних, тоді як лінійна регресія забезпечує гідне якість.

Щоб запобігти перенавчанню, ми часто використовуємо методи регуляризації, такі як ласо та гребінь. Ідея полягає в тому, щоб додати суму модулів ваги і суму квадратів ваг, відповідно, до нашої функції втрат. Прочитайте великий підручник з цих алгоритмів наприкінці статті.

Логістична регресія

Чи не плутайте ці алгоритми класифікації з методами регресії через використання «регресії» в назві. Логістична регресія виконує двійкову класифікацію, тому марковані виходи є двійковими. Визначимо P (y = 1 | x) як умовну ймовірність того, що вихід y дорівнює 1 за умови, що заданий вхідний вектор-функція x. Коефіцієнти w – це ваги, які модель хоче вивчити.

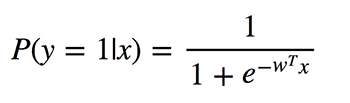
Оскільки цей алгоритм обчислює ймовірність приналежності до кожного класу, ви повинні враховувати, наскільки ймовірність відрізняється від 0 або 1 і усереднює його по всіх об'єктах, як це було з лінійною регресією. Така функція втрат є середнім значенням крос-ентропії:

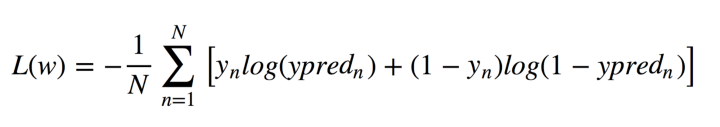
Не панікуйте! Я полегшу це для вас. Дозвольте y мати правильні відповіді: 0 або 1, y_pred - передбачені відповіді. Якщо y дорівнює 0, то перший доданок при сумі дорівнює 0, а другий менше, ніж ми передбачили y_pred до 0 згідно з властивостями логарифму. Аналогічно, якщо y дорівнює 1.

Що хорошого у логістичній регресії? Він приймає лінійну комбінацію функцій та застосовує до неї нелінійну функцію (сигмоподібну), тому це дуже маленький екземпляр нейронної мережі!

Дерева прийняття рішень

Інший популярний і простий у розумінні алгоритм – це дерева рішень. Їх графіка допоможе вам зрозуміти, що ви думаєте, і їхній двигун вимагає систематичного документованого процесу мислення.

Ідея цього алгоритму досить проста. У кожному вузлі ми вибираємо найкращий варіант між усіма функціями та всіма можливими точками поділу. Кожен варіант вибирається таким чином, щоб максимізувати певний функціонал. У деревах класифікації ми використовуємо крос-ентропію та Gini індекс. У деревах регресії ми мінімізуємо суму квадратичної помилки між передбачувальною змінною цільових значень точок, що потрапляють у цю область, і тієї, яку ми присвоюємо їй.

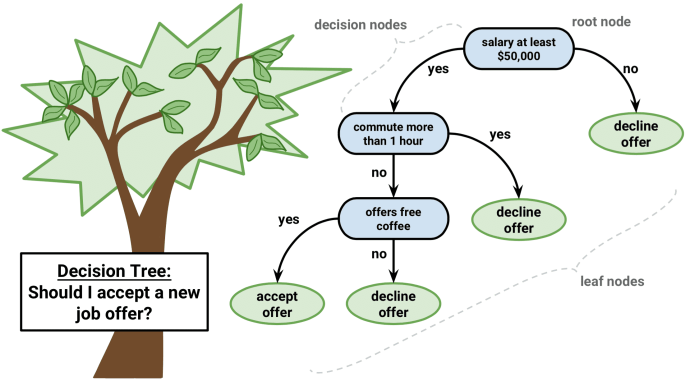
Ми робимо цю процедуру рекурсивно для кожного вузла та закінчуємо, коли ми відповідаємо критеріям зупинки. Вони можуть змінюватись від мінімальної кількості листя у вузлі до висоти дерева. Окремі дерева використовуються дуже рідко, але за складом з багатьма іншими вони створюють ефективні алгоритми, такі як випадкове збільшення лісу або градієнта.

Метод k-середніх

Іноді вам нічого не відомо про властивості, і ваша мета - призначати властивості відповідно до особливостей об'єктів. Це називається завданням кластеризації.

Припустимо, що ви хочете розділити всі об'єкти даних на k кластерів. Вам потрібно вибрати випадкові k точок з ваших даних і назвати їх центрами кластерів. Кластери інших об'єктів визначаються найближчим центром кластеру. Потім центри кластерів перетворюються і повторюється до збіжності.

Це найчіткіша техніка кластеризації, але вона, як і раніше, має деякі недоліки. Перш за все, ви повинні знати низку кластерів, які ми не можемо знати. По-друге, результат залежить від точок, випадково вибраних на початку, і алгоритм не гарантує, що ми досягнемо глобального мінімуму функціоналу.

Існує ряд методів кластеризації з різними перевагами та недоліками, які ви могли б вивчити в читанні, що рекомендується.

Аналіз основних компонентів

Ви коли-небудь готувалися до важкого іспиту вночі чи навіть вранці, перед тим, як він почнеться? Неможливо запам'ятати всю необхідну інформацію, але хочете максимізувати інформацію, яку ви можете запам'ятати за доступний час; наприклад, спочатку вивчити теореми, які зустрічаються у багатьох іспитах тощо.

Аналіз основних компонентів ґрунтується на цій самій ідеї. Цей алгоритм забезпечує зменшення розмірності. Іноді у вас є широкий спектр функцій, які, ймовірно, сильно корелювалися між собою, а моделі можуть легко перевантажувати величезні обсяги даних. Потім ви можете застосувати цей алгоритм.

Дивно, але ці вектори є власними векторами кореляційної матриці ознак набору даних.

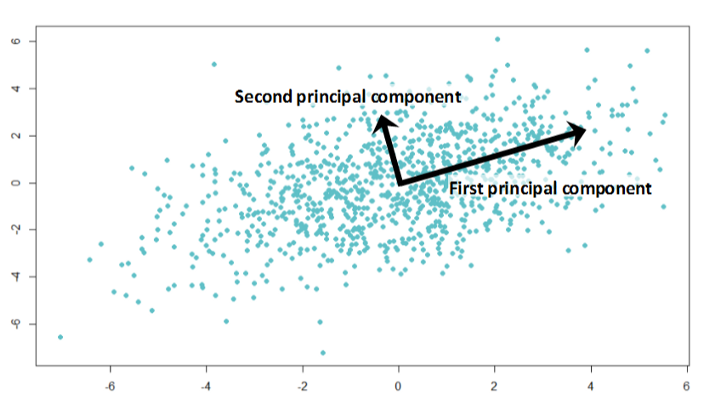
Тепер алгоритм зрозумілий:

• Ми обчислюємо кореляційну матрицю стовпців ознак та знаходимо власні вектори цієї матриці.
• Ми беремо ці багатовимірні вектори та обчислюємо проекцію всіх ознак на них.

Нові функції - координати від проекції, які число залежить від кількості власних векторів, у яких ви розраховуєте проекцію.

Нейронні сіті

Я вже згадував про нейронні мережі, коли ми говорили про логістичну регресію. Існує безліч різних архітектур, які цінні у конкретних завданнях. Найчастіше це діапазон шарів або компонентів з лінійними з'єднаннями між ними та наступними нелінійностями.

Якщо ви працюєте з зображеннями, гнучкі гнучкі нейронні мережі показують відмінні результати. Нелінійності представлені згортковими шарами, що об'єднують, здатними фіксувати характерні особливості зображень.

Для роботи з текстами та послідовностями вам краще вибрати рекурентні нейронні мережі (англ. Recurrent neural network ; RNN ). RNN містять модулі довгої короткострокової пам'яті або керованих рекурентних нейронів і можуть працювати з даними, для яких ми знаємо заздалегідь розмір. Одним з найбільш відомих програм RNN є машинний переклад.

Висновок

Я сподіваюся, що ви тепер розумієте загальні уявлення про найбільш використовувані алгоритми машинного навчання і маєте інтуїцію в тому, як вибрати один із них для вашого конкретного завдання. Щоб полегшити роботу, я підготував структурований огляд їх основних функцій:

• Лінійна регресія і лінійний класифікатор : незважаючи на простоту, вони дуже корисні при величезній кількості функцій, де кращі алгоритми страждають від перенавчання.
• Логістична регресія : найпростіший нелінійний класифікатор з лінійною комбінацією параметрів та нелінійною функцією (сигмоїд) для двійкової класифікації.
• Дерева прийняття рішень : часто подібні до процесу прийняття рішень людьми і легко інтерпретуються, але найчастіше використовуються в таких композиціях, як випадкове зростання лісу або градієнта.
• Метод k-середніх : більш примітивний, але дуже простий у розумінні алгоритм, який може бути ідеальним як основа у безлічі завдань.
• Аналіз основних компонентів : відмінний вибір для зменшення розмірності вашого простору з мінімальною втратою інформації.
• Нейронні мережі : нова ера алгоритмів машинного навчання, які можуть застосовуватися для багатьох завдань, але їхнє навчання потребує величезної обчислювальної складності.

Рекомендована література

• Огляд методів кластеризації
• Повний підручник з регресії хребтів та ласо в Python
• Youtube канал про AI для початківців з відмінними посібниками та прикладами

Стаття написана: Daniil Korbut | Жовтень 27, 2017р.