Иногда перед нами встает задача найти минимальный путь от точки А до точки В . "Карта передвижения" может иметь преграды и быть подобием лабиринта. Подобные задачи встречаются при разработке игр, проектировании печатных плат и разработке GPS-навигаторов и т.д.
Алгоритмов поиска минимального пути большое множество. Но, наиболее простым и эффективным является Алгоритм волновой трассировки (Алгоритм Ли) , который основан на методах поиска в ширину.
В работе данного алгоритма не сложно разобраться. Он будет понятен даже новичку в программировании.
Я буду приводить пример своей работы. У меня имеется подобие клеточного автомата (граф, состоящий из узлов и ребер между ними). На нем будем реализовывать Алгоритм Ли .
Реализация алгоритма состоит из 3-х этапов:
- Инициализация начальных данных;
- Распространение волны;
- Восстановление пути.
Первый этап - Инициализация начальных данных
Вам нужно иметь массив объектов (узлов, ячеек). У меня это класс Node .
Каждый объект, кроме иных, имеет поле near типа, например, ArrayList. В данное поле вы записываете всех "соседей" ( соседние узлы данного узла ).
Каждый узел получает отметку "проходимый / непроходимый".
Записываются стартовый и финишный узлы.
Второй этап - Распространение волны
Вы должны иметь численный массив (по количеству ячеек), куда будут записываться числа (отметки) для каждой ячейки. По умолчанию все значения ячеек равны нулю.
Стартовый узел
получает значение 1.
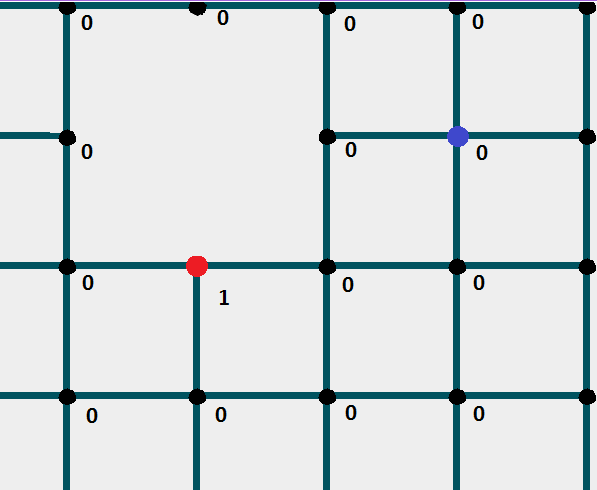
Проверяете все "соседние" узлы данного узла на "проходимость", и проверяете нет ли на них уже отметки. Так как отметка должна ставиться только один раз.
Если все удовлетворительно ставите отметку на 1 больше , чем у предыдущего узла. Далее проверка его "соседних узлов".
Так до тех пор, пока не дойдете до финишной ячейки .
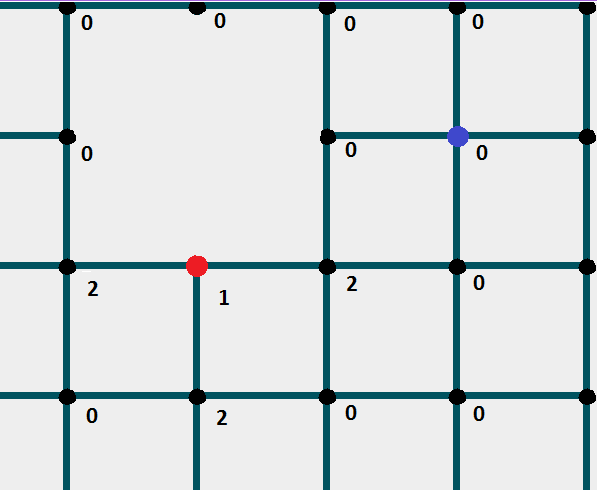
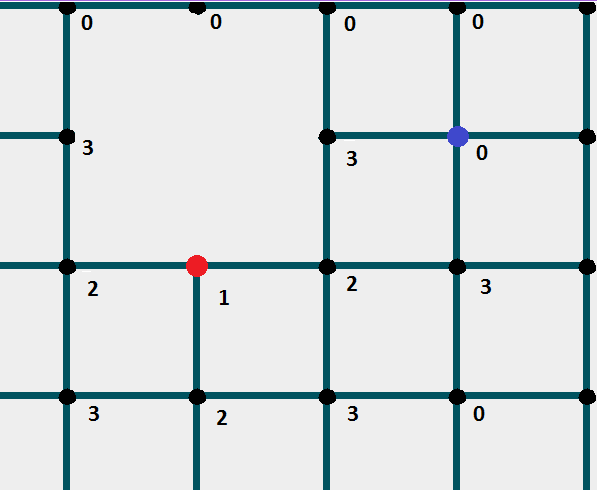
Пример кода:
- public int[] WavePropagation(int fromNode, int toNode, ElementManager elementManager) { // распространение волны
- int[] markedNode = new int[elementManager.GetNumberOfAllNodes()]; // массив, где будут хранится "отметки" каждого узла
- int markNumber = 1; // счетчик
- markedNode[fromNode] = markNumber; // инициализация стартового узла
- while (markedNode[toNode] == 0) { // пока не достигли финишного узла
- for (int i = 0; i < markedNode.length; i++) {
- if (markedNode[i] == markNumber) { // начинаем со стартового узла
- for (int j = 0; j < elementManager.GetNode(i).near.size(); j++) { // просматриваем все соседние узлы
- if(markedNode[elementManager.GetNode(i).near.get(j).number] == 0 // если он еще не получил "отметку"
- && elementManager.GetNode(i).near.get(j).isEnable){ // если доступен
- markedNode[elementManager.GetNode(i).near.get(j).number] = (markNumber + 1);
- }
- }
- }
- }
- markNumber++;
- }
- return markedNode;
- }
Третий этап - Восстановление пути
В массив пути заносите финишный узел .
Просматриваете отметки всех узлов, "соседних" к финишному узлу. Заносите в массив пути тот узел, отметка которого на 1 меньше , чем у финишного узла.
Повторяете это действие, пока не будет достигнут стартовый узел .
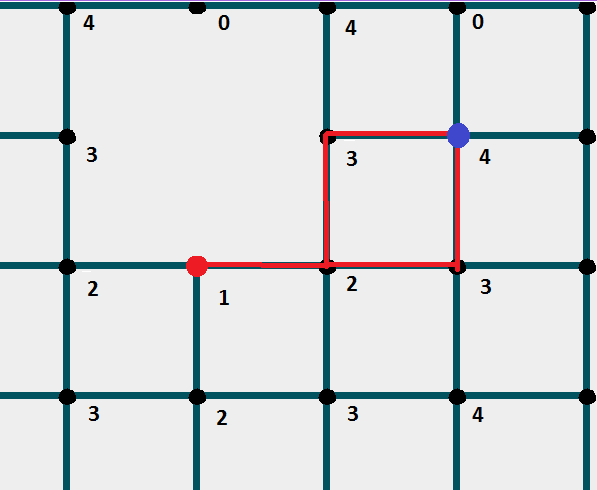
Пример кода:
- public ArrayList<Integer> PathRecovery(int fromNode, int toNode, int[] markedNode, ElementManager elementManager) { // восстановление пути
- ArrayList<Integer> paramsPaveTheRoute = new ArrayList<>(); // массив, где хранится путь
- if (markedNode[elementManager.GetNode(toNode).number] != 0) { // еще раз проверяем дошел ли алгоритм до финишного узла
- paramsPaveTheRoute.add(toNode); // добавляем финишный узел к пути
- ElementManager.Node currentNode = elementManager.GetNode(toNode);
- while (currentNode.number != fromNode) { // пока не дошли до стартового узла
- for (int i = 0; i < currentNode.near.size(); i++) { // проверяем соседние узлы
- if (markedNode[elementManager.GetNode(currentNode.near.get(i).number).number]
- == markedNode[currentNode.number] - 1) { // если значение пометки узла на 1 меньше, чем у предыдущего узла
- currentNode = elementManager.GetNode(currentNode.near.get(i).number); //узел становится текущим
- paramsPaveTheRoute.add(currentNode.number); // заносится в массив
- }
- }
- }
- }
- return paramsPaveTheRoute;
- }
Результат работы программы:
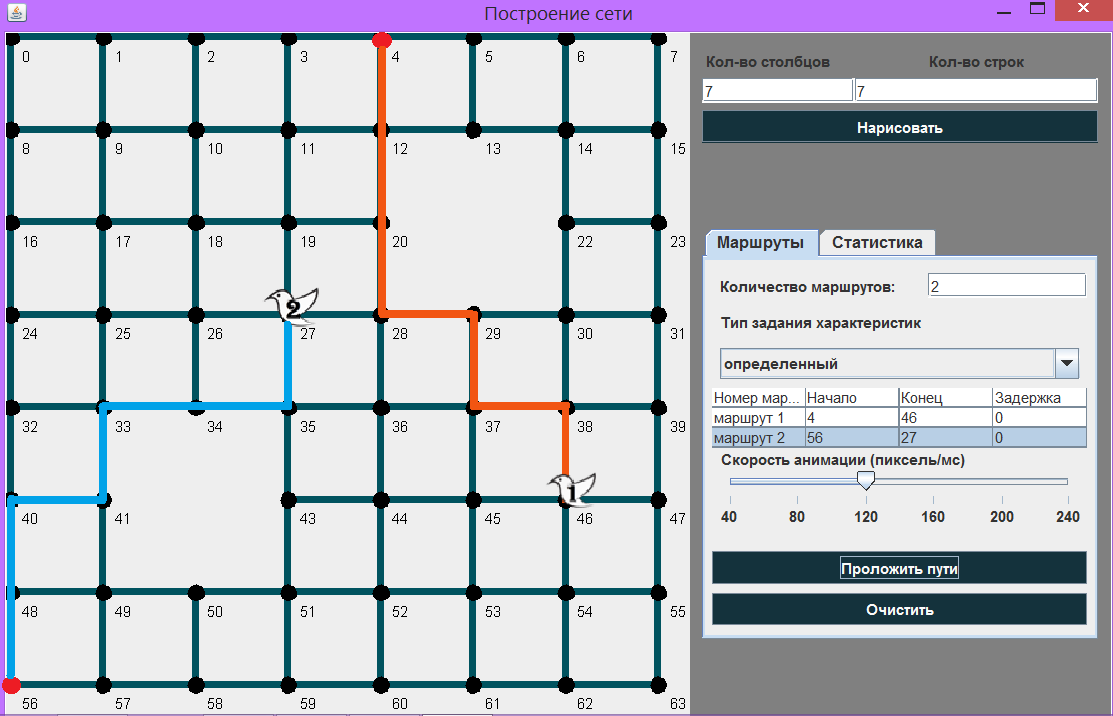
Таким образом, я думаю, вы убедились, что Алгоритм Волновой трассировки (Алгоритм Ли) совсем не сложен для реализации. Он выполняет поиск минимального пути, делая небольшое количество вычислений. При желании, данный универсальный алгоритм можно усложнить.
