Различают модовую дисперсию, которая обусловлена большим количеством мод в оптических волокнах , а также хроматическую дисперсию, связанную с некогерентностью источников излучения, реально работающих в определенном спектре длин волн.
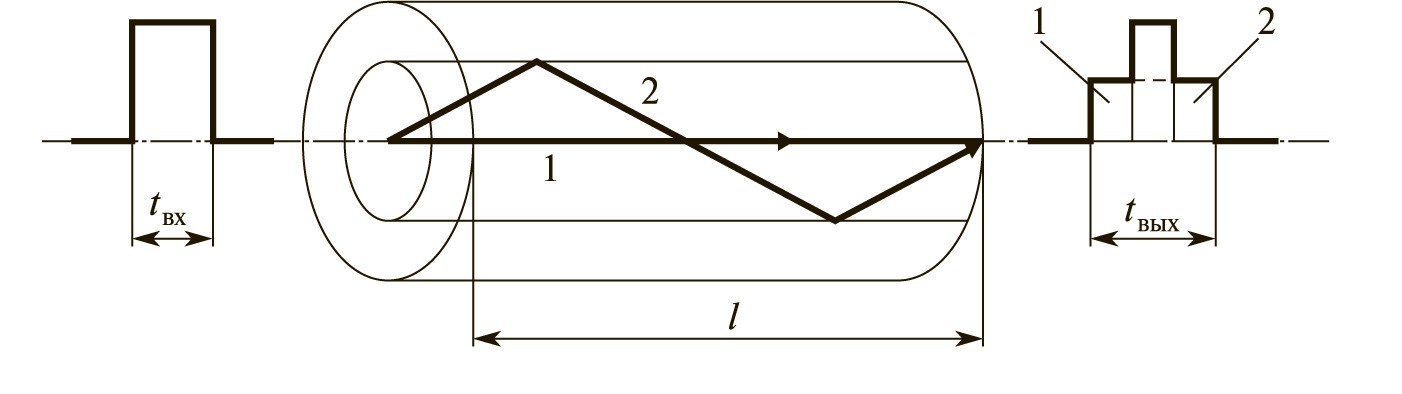
Рассмотрим распространение многомодового светового луча вдоль световода. В данном случае имеется две моды, два луча. Первый распространяется вдоль продольной оси световода, тогда как второй отражается от границ раздела сред. Таким образом путь прохождения второго светового луча будет больше, чем первого. В итоге когда эти два луча, переносящие электромагнитную энергию, складываются вместе, наклонный луч по сравнению с аксиальным лучом имеет временное запаздывание, которое рассчитывается по следующей формуле:
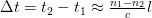
c
– скорость распространения света
l
– длина оптического волокна
n
1
,
n
2
– коэффициенты преломления сердечника и оболочки
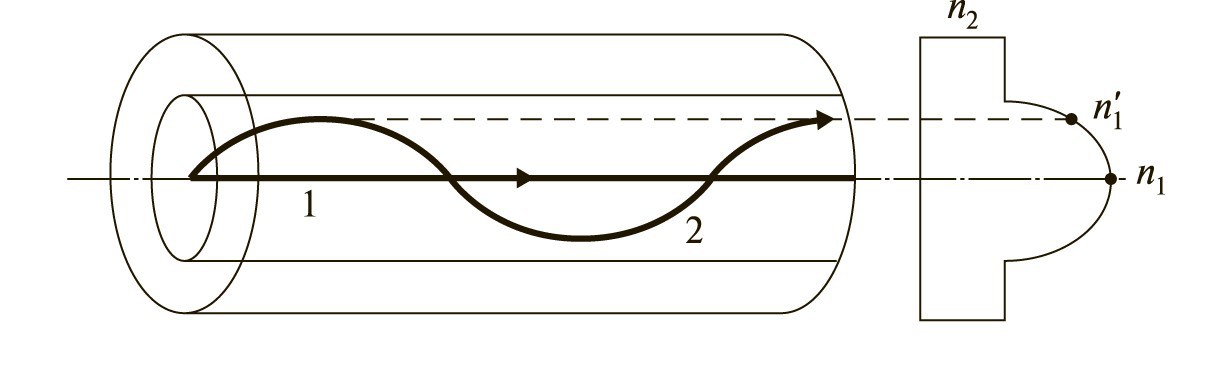
Модовая дисперсия градиентных оптических волокон, как правило, на два порядка ниже, чем у волоконных световодов со ступенчатым профилем показателя преломления. За счет плавного изменения показателя преломления сердечника волоконного световода уменьшается путь прохождения второго луча вдоль волокна. Вследствие чего уменьшается время запаздывания второго луча относительно первого.
В одномодовых оптических волокнах модовая дисперсия отсутствует и увеличение длительности импульса определяется хроматической дисперсией, которая, в свою очередь, подразделяется на материальную и волноводную.
Материальной дисперсией называют явление зависимости абсолютного показателя преломления вещества n от длины волны света ( n =ϕ λ() ). Волноводная дисперсия определяется зависимостью коэффициента фазы β от частоты ( β=ϕ ω() ).
Уширение импульса за счет хроматической дисперсии рассчитывается по формуле:
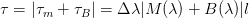
τ
m
– уширение импульса за счет материальной дисперсии, пс;
τ
B
– уширение импульса за счет волноводной дисперсии, пс;
∆λ
– ширина спектра источника излучения, нм;
М(λ)
– коэффициент удельной материальной дисперсии, пс/нм·км;
В(λ)
– коэффициент удельной волноводной дисперсии, пс/нм·км.
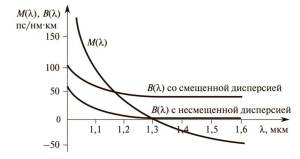
Рассмотрим действие материальной и волноводной дисперсий в одномодовом волокне. Как видно из графика, при увеличении длины волны материальная дисперсия уменьшается, а на длине волны 1,31 мкм становится равна нули. Длина волны в таком случае считается длиной волны нулевой дисперсии. При этом свыше 1,31 мкм дисперсия становится отрицательной. Волноводная дисперсия несмещенных волокон представляет собой относительно небольшую величину и находится в области положительных чисел. При разработке оптических волокон со смещенной дисперсией, в основе которой находится волноводная компонента, пытаются компенсировать материальную дисперсию в длинноволновую область, т.е. к третьему окну прозрачности (λ = 1,55 мкм). Данный сдвиг осуществляется уменьшением диаметра сердцевины, увеличением ∆ и использованием треугольной формы профиля показателя преломления сердцевины.
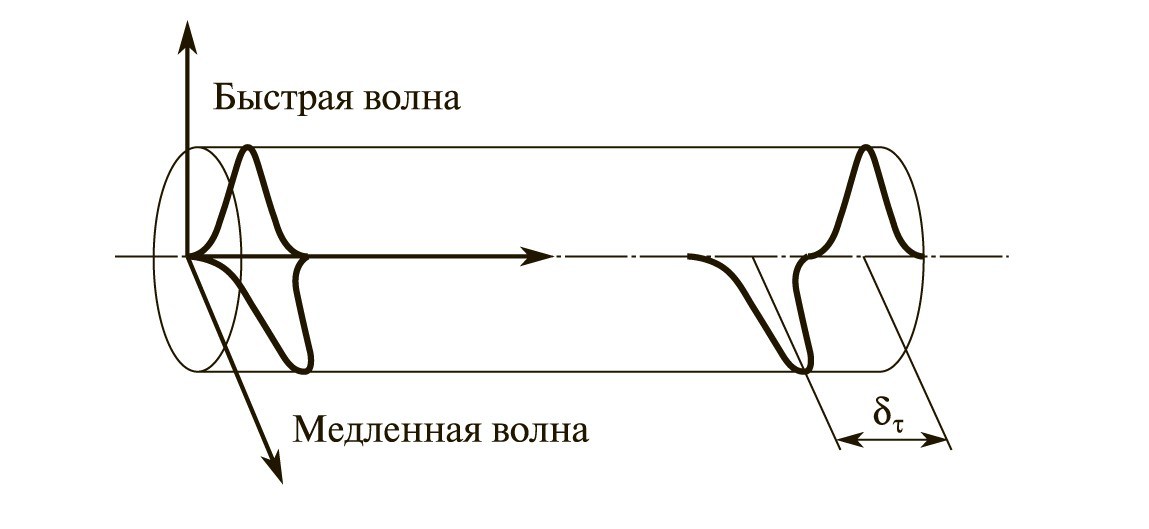
При распространении поляризованной световой волны вдоль оптического волокна возникает поляризационная дисперсия. Световая волна с точки зрения волновой теории представляет собой постоянно изменяющиеся магнитное и электрическое поля, вектор которых расположен перпендикулярно распространению электромагнитной (световой) волны. Примером световой волны может служить естественный свет, у которого направление электрического вектора изменяется случайным образом. Если излучение монохроматическое и векторы колеблются с некоторой постоянной частотой, то их можно представить в виде суммы двух взаимно перпендикулярных составляющих х и у. Идеальное оптоволокно является изотропной средой, в которой электромагнитные свойства являются одинаковыми во всех направлениях, например показатели преломления. Среда с различными показателями преломления в двух ортогональных осях x и y называется двулучепреломляющей. При этом волокно в данном случае по прежнему остается одномодовым, поскольку две ортогонально поляризованных моды имеют одну и ту же постоянную распространения. Но это справедливо лишь для идеального оптического волокна.
В реальном оптическом волокне две ортогонально поляризованные моды имеют неидентичные постоянные распространения, вследствие чего появляется временная задержка и происходит уширение оптического импульса.
Уширение импульса за счет поляризационной модовой дисперсии (PMD) рассчитывается по формуле:
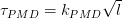
Таким образом, поляризационная модовая дисперсия проявляется исключительно в одномодовых оптических волокнах с нециркулярной (эллиптической) сердцевиной и при определенных условиях становится соизмеримой с хроматической. Поэтому результирующая дисперсия одномодового оптического волокна определяется следующей формулой:
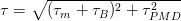
Дисперсия существенно ограничивает пропускную способность волоконных световодов. Максимальная ширина полосы пропускания на 1 км оптической линии приближенно рассчитывается по формуле:
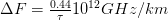
τ — уширение импульса, пс/км.
